大家好，這里是大話硬件！

根據前天分享的文章，分析了ADC轉換的過程，在評價ADC性能時有5個靜態指標和5個動態指標評價ADC。可以作為選型時以及理論計算時的參考。

靜態性能指標包括：失調誤差，增益誤差，微分非線性誤差（DNL），積分非線性誤差（INL），絕對精度誤差。動態性能指標包括：信噪比，信噪失真比，無雜散動態范圍，有效位，總諧波失真。

今天這篇文章我們來看看第一個靜態性能指標——失調誤差。

靜態性能指標意味這種誤差只要存在，就會影響ADC的每一個編碼。失調誤差定義為傳遞函數無法通過零點的模擬值。失調誤差也稱為偏置誤差，這種誤差反映的是第一個標準偏置點和第一個實際偏置點之間的誤差。如下圖虛線所示理想ADC和實線代表實際ADC所示的轉換函數。

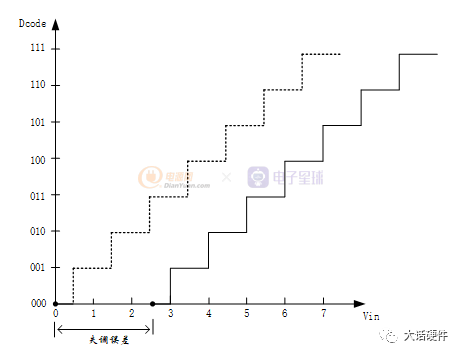
理想ADC轉換函數輸出代碼為000時，輸入電壓在0~0.5LSB范圍內，實際轉換函數輸出代碼為000時，輸入電壓在2.5~3.0LSB范圍內，因此，失調誤差是2.5LSB。

用數學關系的思路來理解失調誤差。假設輸入模擬信號是x，輸出數字代碼是y，在不考慮±0.5LSB的條件下，輸入信號和輸出代碼之前應該存在下面的關系式：

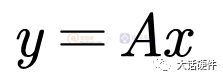
即輸入信號和輸出代碼之間是線性的，用紅色來表示它們之前的線性關系。

在不存在失調誤差時，整數點1，2，3……6，7是跳變點。如果此時存在失調誤差，則輸入信號和輸出信號之前的關系式成為了：

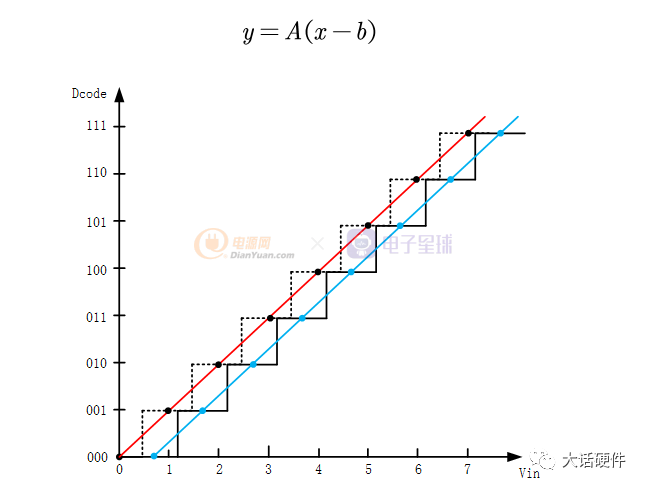
從傳輸函數可以看出，失調誤差為0時，輸出是000時，輸入信號在0~0.5LSB以內；若存在失調誤差，輸出是000時，輸入信號在0~1.25LSB以內，即引入的失調誤差是0.75LSB。

用數學關系式看上述的關系類似傳輸函數向右平移了0.75LSB的單位長度。這種平移的失調誤差，將會影響到每一個代碼的輸出，編碼跳變從之前的1，2，3….6，7，變成了現在的1.75，2.75，3.75……6.75，7.75。

因此，從數學的角度看失調誤差，就像是一次函數的截距。如果截距為負，輸入電壓會在大于0.5LSB以后才發生跳變，如上述所示的0.75SB處產生第一個編碼跳變，此時的失調誤差稱為負失調誤差。可想而知負失調誤差過大，會導致較大范圍的輸入電壓條件下，輸出均為0，數字編碼用幾個輸入就已經滿量程，限制了數字編碼的量程。

同理可知，如果截距為正，輸入電壓會在小于0.5LSB之前就發生跳變，如下圖所示，輸入電壓小于0.5LSB時，輸出數字代碼為010，則會導致輸入電壓還未滿量程時，數字代碼就達到了飽和。

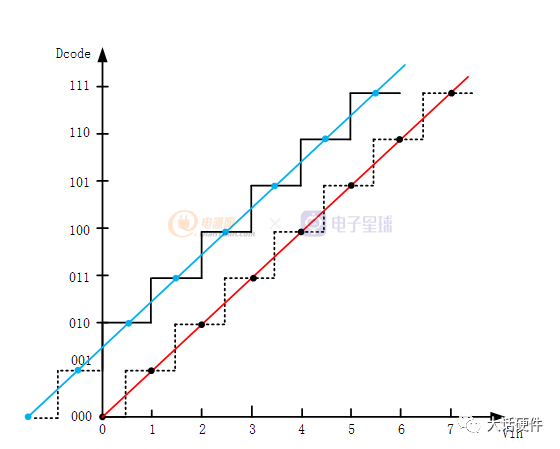
總結一下：無論是正失調偏差會影響數字編碼的量程，負失調偏差會影響模擬輸入量程。根據上面的分析，可以得到矯正的ADC失調誤差的方法，在反方向上補償對應的偏差就能使傳輸函數的截距為0，即失調誤差為0。