上節我們講的主要觀點是:信號在我們腦海里面應該是以頻譜的方式呈現,也就是各種頻率的正弦波。
原因也說了,電感和電容的阻抗公式只能適用于正弦波。而正巧的是,傅里葉變換能將任何信號都變成正弦波的疊加。因此,我們處理信號正確的方式是,先將信號變成各種信號正弦波,然后通過電路,再合并起來,就是我們最終的信號。我舉了方波通過RC濾波器之后波形的例子。

不過呢,上節我并沒有做實驗認證,這次就來補上,本節主要內容也是做實驗的過程,主要是使用Matlab編程,并找了網友焊接的RC濾波器電路板實驗,互相印證。
網友的電路實測的帖子,文末會給出鏈接,下面詳細介紹下。
理論基礎
目的:確定方波通過RC低通濾波器之后的精確波形

我們按照上面思路求得輸出波形公式,過程如下:

公式看著有那么點復雜,其實不難,幅度按照比值代入。需要注意的是,要想得到精確波形,僅僅算出各個頻率的幅度大小還不行,還得帶上相位變化,如此才是準確的。
Matlab代碼:
%參數設置
R=1000/(2*pi); %電阻值,2*pi只是為了方便是截止頻率為整數
C=0.000001; %電容
Fc=1/(2*pi*R*C); %RC濾波器的截止頻率
f=1; %方波頻率1Hz
omega=2*pi*f; %基頻角頻率w
%計算
t=-1:0.001:1 %坐標軸從-1到1,分辨率為0.001
n=[1:2:201]; %表示201諧波數的疊加 單行矩陣:1,3,5,7,9...201
An=4./(pi*n); %方波的各個諧波的系數 單行矩陣:1,1/3,1/5,1/7,1/9...1/201
Bn=sin(omega*n'*t); %方波的各個諧波分量 單列矩陣:sin(wt),sin(3wt),sin(5wt)...sin(201wt) '表示矩陣轉置,即行矩陣變成列矩陣
s_wave=An*Bn; %方波表達式:單行矩陣乘以單列矩陣,即使方波的表達式(諧波系數乘以對應諧波分量,然后相加)
figure; %畫圖
plot(t, s_wave);%繪制方波曲線
hold on;
Cn= (1./(1+R^2*omega^2*(n'.^2)*C^2).^0.5).*sin(omega*n'*t-atan(R*C*omega*n')); %計算各個諧波分量通過濾波器,并附入相移atan(R*C*omega*n');
%Cn= (1./(1+R^2*omega^2*(n'.^2)*C^2).^0.5).*sin(omega*n'*t-atan(R*C*omega*n')); %計算各個諧波分量通過濾波器,并附入相移atan(R*C*omega*n');
rc_wave=An*Cn; %通過RC濾波器的
plot(t, rc_wave);
title(['截止頻率=',num2str(Fc)]); %標題顯示截止頻率是多少執行結果
1Hz方波,通過截止頻率為1Hz的低通濾波器波形:
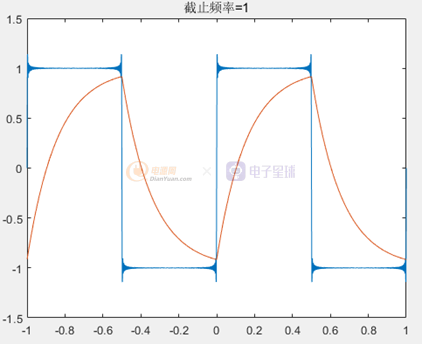
正巧我在某帖子上面看到,有人做過周期矩形波通過低通濾波器的實驗
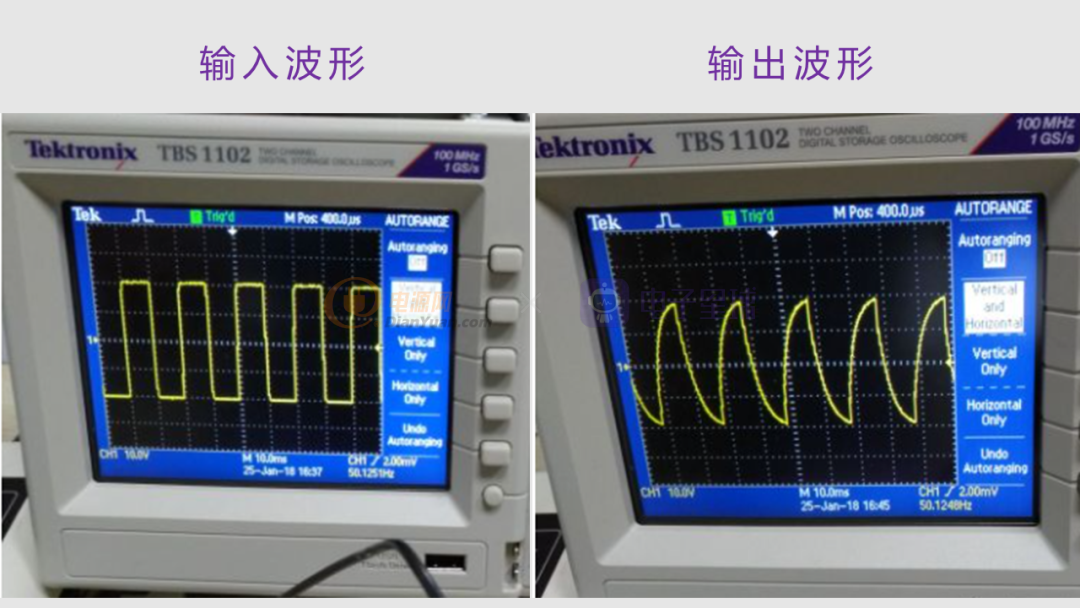
兩個實驗的結果是同樣的,證明了理論的正確性。感興趣的同學,可以修改代碼中的R和C的值,看看方波通過不同截止頻率的波形是分別是什么樣的。
有人說方波通過低通濾波器之后變成了正弦波,顯然也不是的。
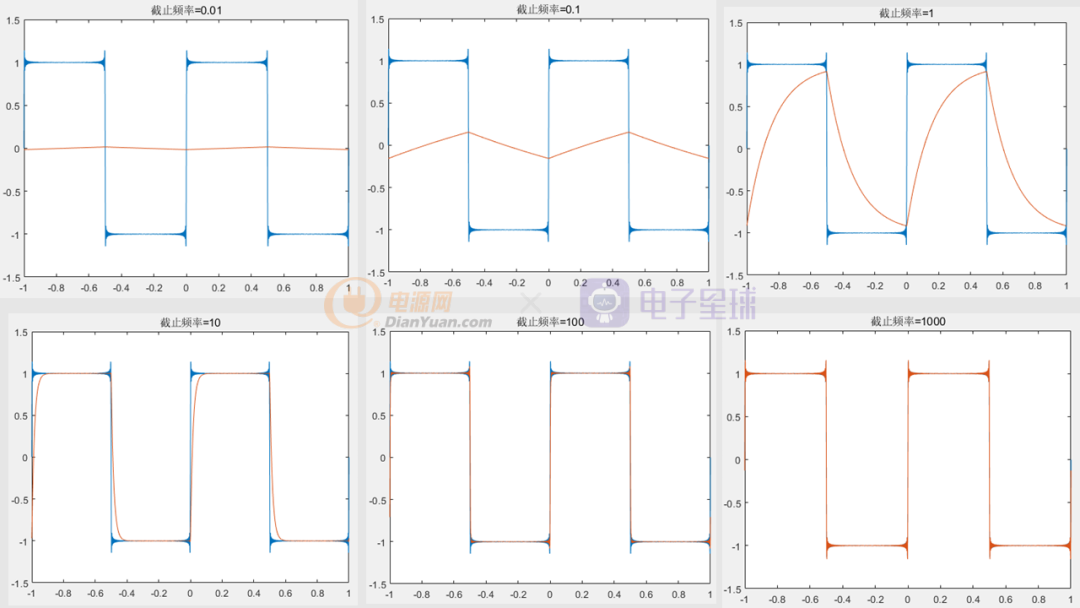
結語
傅里葉變換應用是非常廣泛,寫這個文章的目的,是為了讓同志們知道傅里葉變換是怎么用的,為什么要用這個,這是我的目的。
如果您還是在校生,如果這篇文章能讓你知道為什么要學習傅里葉變換,那我很欣慰。想當初我在學校的時候,僅僅只是因為要考試才去學。


