上一篇我們對LLC的模型進行分析和等效模型的建立,本文將根據模型中的電氣特性,分析LLC如何工作使得輸出穩定的?穩定的輸出是由哪些量決定的?這些量之間又存在哪些關系呢?
在了解上述問題之前,我們先要分析一下電氣變量的關系。【接上一篇文章】
在輸入側,方波電壓(Vsq)的基波電壓為:

它的RMS為:

在輸出端,由于 Vso 近似為方波,因此基波電壓為:
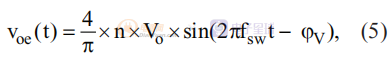
其中 φV 是 Voe 和 Vge 之間的相位角,RMS 輸出電壓為:

對應于 Voe 和 Ioe 的電流的基波分量是:
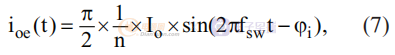
其中 φi 是 ioe 和 voe 之間的相位角,RMS 輸出電流為:

那么交流等效負載電阻 Re 可以計算為:

由于圖 1b 中的電路是單頻正弦交流電路,因此可以按照與所有正弦電路相同的方式進行計算。 角頻率為:

化簡得到:

Cr、Lr 和 Lm 的容抗和感抗分別為:

勵磁電流有效值為:

串聯諧振電路中的循環電流為:

建立電氣變量的關系后,下一步是進行電壓增益函數推導。
自然,輸入電壓和輸出電壓之間的關系可以用它們的比率或增益來描述:
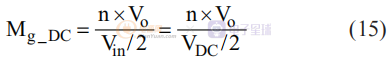
如前所述,將直流輸入電壓和輸出電壓轉換為開關模式,然后等式(15)可以近似為雙極方波電壓(Vso)與單極方波電壓(Vsq)之比:

交流電壓比 Mg_AC 可以通過使用基本分量 Vge 和 Voe 分別代替方程(16)中的 Vsq 和 Vso 來近似:

為簡化符號,此處將使用 Mg 代替 Mg_AC。 從圖 1b 中,Voe 和 Vge 之間的關系可以用電參數 Lr、Lm、Cr 和 Re 來表示。 然后輸入到輸出電壓增益或電壓傳遞函數變為:

等式 (18) 描述了從輸入電壓 (Vin) 到輸出電壓 (Vo) 的連接,該連接與具有 LLC 電路參數的 Mg 相關。 雖然這個表達式只是近似正確,但實際上它足夠接近串聯諧振附近。 接受近似為準確允許方程(19)寫成:

換句話說,可以在知道 Mg、n 和 Vin 之后確定輸出電壓。
電壓增益函數的歸一化格式
等式 (18) 描述的電壓增益函數以具有絕對值的格式表示。 很難對這種格式的設計問題進行一般性描述。 最好用規范化的格式來表達。 為此,可以選擇串聯諧振頻率 (f0) 作為歸一化的基礎。 然后歸一化頻率表示為:

此外,為了將兩個電感合二為一,電感比可以定義為:

串聯諧振電路的品質因數定義為:

請注意,fn、Ln 和 Qe 是無單位變量。
在這些定義的幫助下,電壓增益函數可以被歸一化并表示為:
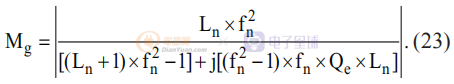
輸入和輸出電壓之間的關系也可以從等式(23)獲得:
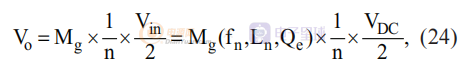
電壓增益函數的特性
等式 (23) 表示的電壓增益函數和圖 1b 中的電路模型構成了本主題所述設計方法的基礎; 因此,有必要了解 Mg 如何作為三個因素 fn、Ln 和 Qe 的函數。 在增益函數中,頻率 fn 是控制變量。 Ln 和 Qe 是虛擬變量,因為它們在確定物理參數后就固定了。 設計完成后,通過 fn 調整 Mg。 因此,解釋增益函數如何表現的一個好方法是在給定條件下從 Ln 和 Qe 的值族中繪制 Mg 與 fn 的關系圖。
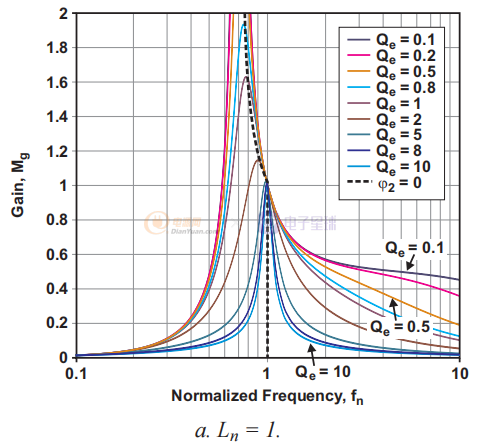
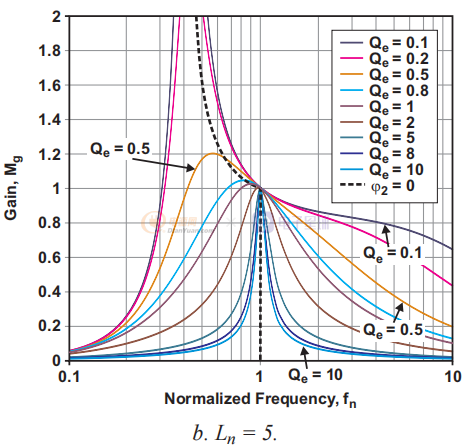
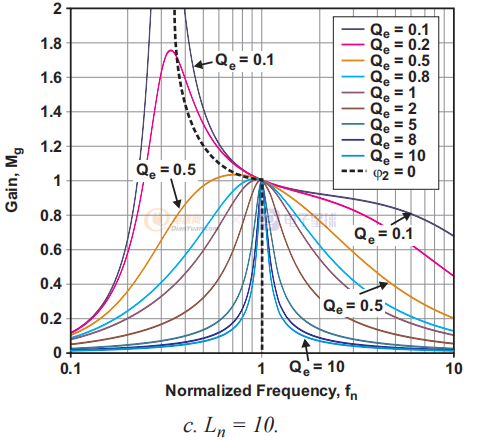

圖 2. 具有不同 Ln 值的電壓增益函數 (Mg) 圖。
圖1a到1d說明了幾種可能的關系。 每個圖都由一個固定的 Ln 值(Ln = 1、5、10 或 20)定義,并針對變量 Qe 顯示具有九個值(從 0.1 到 10)的曲線族。 從這些圖中,可以得出幾個觀察結果。
Mg的值不小于零。 這是顯而易見的,因為 Mg 來自模數運算符,它描述了一個包含實數和虛數的復雜表達式。 這些數字代表幅度和相位角,但在這種情況下只有幅度有用。
在給定的 Ln 和 Qe 內,Mg 在電路諧振頻率附近呈現凸曲線形狀。 這是一條典型曲線,顯示了諧振轉換器的增益形狀。 對應于諧振峰值(fn_c0,或 fsw = fc0)的歸一化頻率隨著負載的變化而移動,因此對于給定的 Ln,也隨著 Qe 的變化而移動。
改變 Ln 和 Qe 將重塑 Mg 曲線并使其與 fn 不同。 由于 Qe 是由方程 (9) 和 (22) 描述的負載函數,因此 Mg 呈現了一系列將頻率調制與負載變化相關聯的曲線。
無論使用 Ln 和 Qe 的哪種組合,所有曲線都會收斂并通過 (fn, Mg) = (1, 1) 點。 該點位于 fn = 1 處,或來自公式 (20) 的 fsw = f0。 根據串聯諧振的定義,在 f0 處 XLr– XCr = 0。 換句話說,Lr 和 Cr 兩端的壓降為零,因此輸入電壓直接施加到輸出負載,從而導致單位電壓增益 Mg = 1。
請注意,工作點 (fn, Mg) = (1, 1) 與負載無關; 即,只要增益 (Mg) 可以保持一致,無論負載電流是多少,開關頻率都將處于串聯諧振頻率 (f0)。 換句話說,在工作點位于 (fn, Mg) = (1, 1) 或其附近的設計中,頻率變化被縮小到最小。 在 (fn, Mg) = (1, 1) 處,假設沒有寄生功率損耗,串聯諧振電路的阻抗為零。 然后,無論負載電流變化多少,整個輸入電壓都會施加到輸出負載。 然而,遠離(fn, Mg) = (1, 1),串聯諧振電路的阻抗變為非零,電壓增益隨著負載阻抗的不同而變化,相應的操作變得依賴于負載。
對于固定的 Ln,增加 Qe 會縮小曲線,導致頻率控制帶變窄,這是預期的,因為 Qe 是串聯諧振電路的品質因數。 此外,隨著整條曲線向下移動,Mg的對應峰值變小,對應于該值的fn向右移動并接近fn=1。這種隨著Qe增加的頻移是由于負載增加。 回顧方程 (9) 和 (22) 很明顯Qe 的增加可能來自 RL 的減少,因為 Lm 和 Lr 都是固定的。 對于相同的串聯諧振頻率,Cr 也是固定的。 RL 與 Lm 平行,因此減少 RL 將減少 Lm 的影響并將 fc0 移向 f0。 作為一個簡單的例子,檢查兩個極端是有幫助的:
1、如果 RL 開路,則 Qe = 0,并且 fc0 = fp,如等式 (2) 所述。 fc0 位于 f0 的最左邊,對應的增益峰值非常高,理論上可以無限大。
2、如果 RL 短路,則 Qe = ∞ 并且 Lm 被完全旁路或短路,使得 Lm 對增益的影響消失。 然后來自 Lm 效應的相應峰值增益值變為零,并且 fc0 一直向右移動,與 f0 重疊。
3、因此,如果 RL 從無窮大變為零,則諧振峰值增益從無窮大變為 1,峰值諧振處的相應頻率 (fc0) 從 fp 移動到串聯諧振頻率 (f0)。
對于固定的 Qe,Ln 的減小會縮小曲線; 整個曲線被擠壓,fc0 向 f0 移動。 這導致更好的頻率控制帶具有更高的峰值增益。 有兩個原因。 首先,當 Ln 由于 Lm 減小而減小時,fp 越來越接近 f0,從而擠壓了從 fp 到 f0 的曲線。 其次,降低的 Ln 會增加 Lr,從而導致更高的 Qe。 如上所述,較高的 Qe 會縮小曲線。
乍一看,Ln 和 Qe 的任何組合似乎都適用于轉換器設計,并且可以在 fn = 1 的任一側運行 fn 來進行設計。但是,下一篇文章會講述LLC在設計時的更多考慮!


