大家好，很高興和各位一起分享我的第三十二篇原創文章，喜歡和支持我的工程師，一定記得給我點贊，收藏，分享喲。想和我進一步探討技術干貨，可以添加微信號（matlab_simulink）。

    對稱分量法是分析不對稱故障的常用方法，根據對稱分量法，一組不對稱的三相量可以分解為正序、負序和零序的三相對稱分量，將電網等效為各分量下的等效序網絡后，就可以對電力系統的各種不對稱運行及不對稱故障情況進行分析。但是，傳統的對稱分量法定義在頻域范圍，用相量表示，在進行對稱分量分析時，需要計算各個相量的模值和相位，故只能應用于電力系統不對稱運行或不對稱故障的穩態分析中，而無法應用于系統的暫態分析。

    而在電力電子裝置控制系統設計過程中，對暫態不對稱運行或者不對稱故障分析格外重要（比如SVG、HVDC等），我們需要各個分量的瞬時值，利用電壓或電流的瞬時值構造相應的無延時旋轉相量，再利用這些旋轉相量進行對稱分量變換，獲取各個序分量的瞬時值。

    在三相電路中，對于任意一組不對稱的三相相量（電壓或電流），可以分解為三組三相對稱的相量，當選擇a相作為基準相時，三相電流相量與其對稱分量之間的關系（以電流為例）為

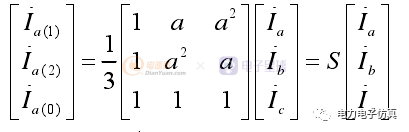
(1)

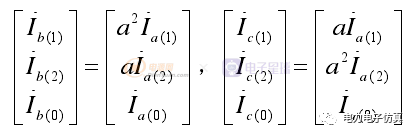
(2)

令三相不對稱電流的瞬時值為

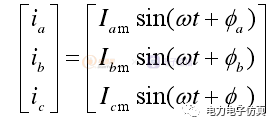
（3）

式中，Ia，Ib，Ic分別表示三相電流的瞬時值；Iam,Ibm,Icm分別表示三相電流的幅值；φa，φb，φc分別表示三相電流的初相位。

設與三相電流Ia，Ib,Ic所對應的旋轉相量分別為

(4)

由上式可知，旋轉相量的虛部的系數就是三相電流的瞬時值，只要求出這些相量的實部就可以確定這些向量。而相量實部的求取可以根據三角函數的關系式，可以求導法完成。 

分別對三相電流求導可得

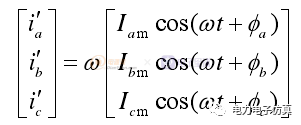
(5)

三相電流的導數是對應旋轉相量實部的ω倍，由此，可以利用導數構造三相電流的旋轉相量。在實際工程的應用中，求導可以在離散數字量的基礎上用差分方法完成，即

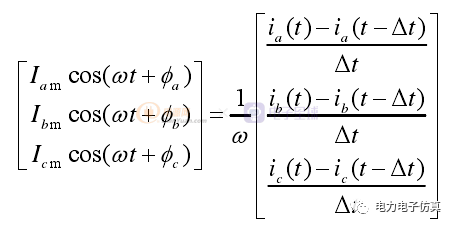
(6)

式中， Δt為計算步長，ia(t)，ib(t) ，ic(t) 分別為三相電流的當前步長的瞬時值；ia(t-Δt)，ib(t-Δt) ，ic(t-Δt)分別為上一步長三相電流的瞬時值。

基于所構造的旋轉相量，將式4代入式1和2，經過整理可分別得到三相電量的正序、負序和零序分量的瞬時值:

整體控制框圖為：

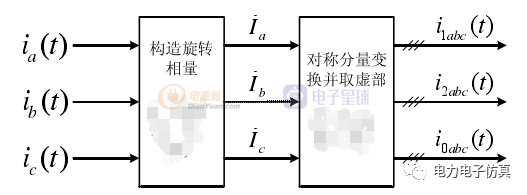
為了驗證上述方法可行性，在simulink搭建一個簡單的三相不對稱電路，電網電壓為380V，三相負載分別為：1Ω+2mH，2Ω+2mH，1Ω+1mH,三角接法。對其電流進行分析，仿真結果如下 ：

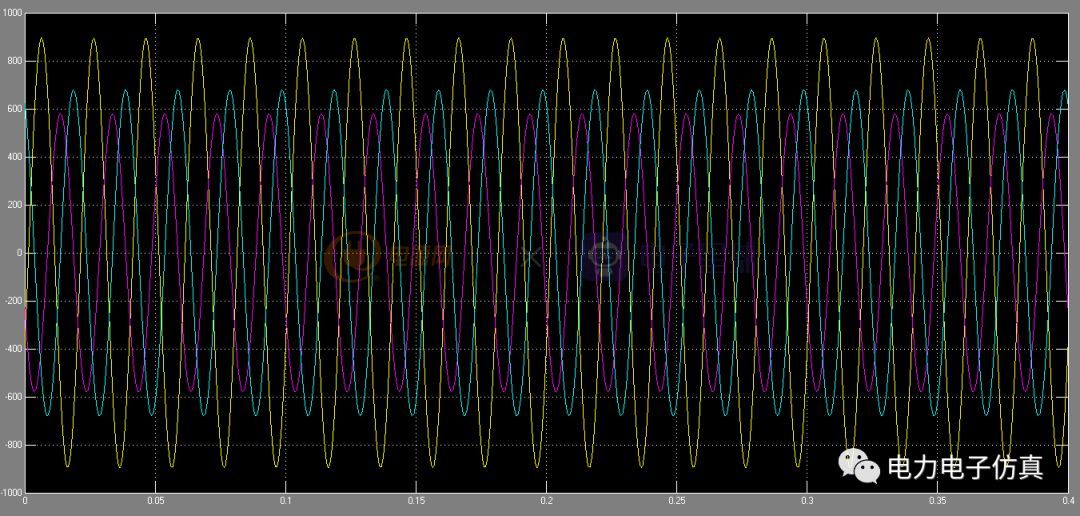
上圖為電網電路，從仿真結果可以看出，由于三相負載不對稱，故三相電流不對稱。

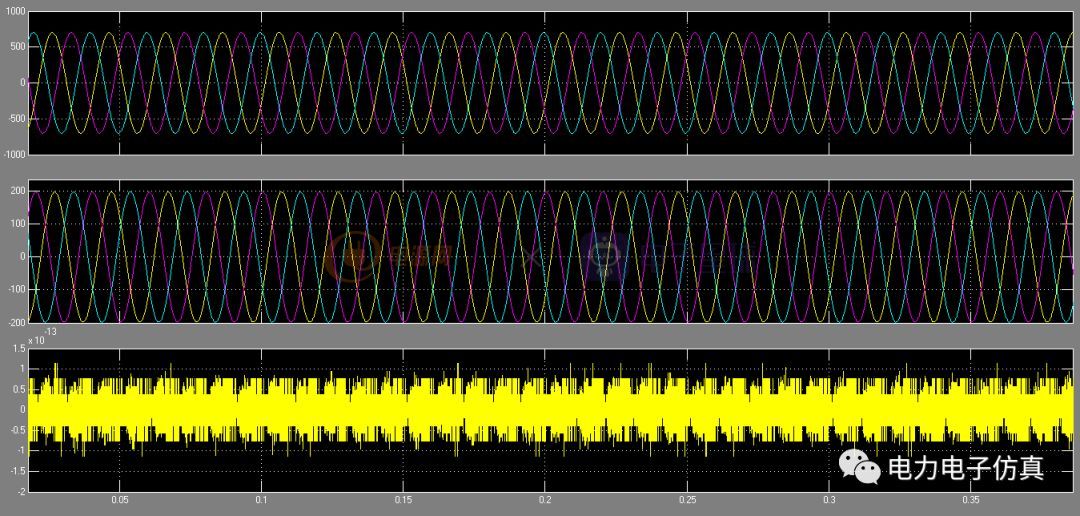
上圖分別為正序、負序和零序的電流，從仿真結果顏色可以看出，第一個仿真結果為正序（順序為藍黃粉），第二個仿真結果為負序（藍粉黃），由于負載為角接，故零序為0，即第三個仿真結果。

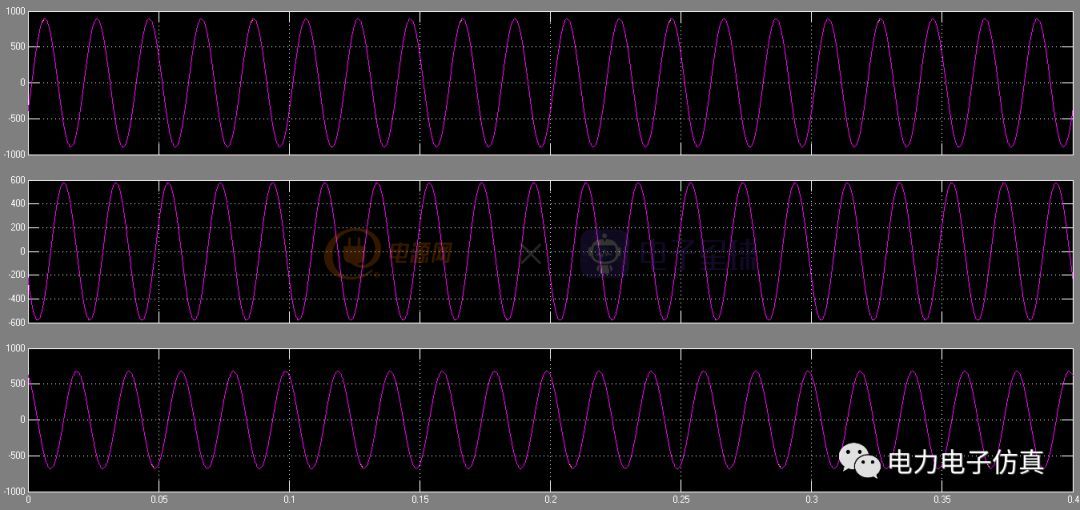
為了驗證分離后的電流正確性，分別將abc三相的正序和負序求和，與原電流進行疊加比較，上圖為ABC三相原電流和正負序電流求和的疊加波形，從仿真結過可以看出，求和值和原電流完全吻合，證明分離后的正序、負序和零序結果正確。