一、原則

當我們沒有方程 H 時，就不可能直接使用反饋設計方法。我們可以或需要使用模擬或測量來獲得設備（或系統(tǒng)）傳遞函數(shù)。

顯而易見的方法是直接測量或模擬設備以對其進行表征。在非線性系統(tǒng)中，設備方程隨連續(xù)（或直流）工作點而變化。在測量過程中，低頻效應，如自熱，會影響工作點并修改設備傳遞函數(shù)。在增益非常高的系統(tǒng)中，甚至可以飽和。當這種情況發(fā)生時，測量不再是在線性區(qū)域中進行，需要采取措施將系統(tǒng)恢復到線性模式。最常用的方法是在閉環(huán)中表征設備。反饋將負責設置工作點。在測量過程中，它將補償?shù)皖l漂移效應，如自熱，并使系統(tǒng)保持在線性區(qū)域。

為了在回路閉合時提取開環(huán)，我們在反饋回路中注入（或添加）一個小信號。注入的信號會擾亂系統(tǒng)。通過測量效果，我們可以得到開環(huán)傳遞函數(shù)。我們獲得以下設置。

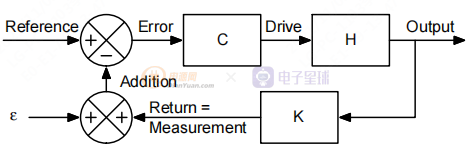圖 7. 測量或模擬設置

在上圖中，代表注入的信號。 我們將返回信號定義為將添加到注入信號的信號。 加法是那個操作的結果。返回也可以看作是注入信號擾動的結果。 帶注入加法器的系統(tǒng)方程如下：

由于我們正在尋找傳遞函數(shù)，我們將使用正弦波信號作為注入信號。 通過改變注入信號的頻率，我們可以確定頻率響應并繪制傳遞函數(shù)的波特圖。

由于參考是直流信號，我們專注于頻率響應。 它可以從圖片中排除，因為它不包含頻率信息。

使用這些假設，我們可以求解（11）中給出的方程以獲得輸出方程。 然而，這還不是最有趣的。 由于我們已經(jīng)“打破”了注入加法器的循環(huán)，我們可以專注于它周圍的信號。 由于 Return 不知何故是注入信號 ε 效應的結果，我們可以求解系統(tǒng)并得到作為 ε 或加法函數(shù)的 Return 方程。我們可以很容易地得到：

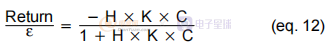
同理可得：

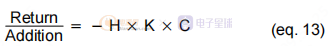
我們可以看到（13）和（12）分別與開環(huán)和閉環(huán)方程相反。 這是因為從理論上講，比較器不在圖片范圍內，而是充當“回路斷路器”。 在測量或仿真設置中，注入加法器的作用是在該點“中斷”循環(huán)，而比較器則保持不變。

二、分析

注入加法器可以放置在循環(huán)中的任何位置，等式（13）和（12）仍然有效。有三種簡單的方法可以制作一個簡單的注入加法器：

1. 與浮動電源串聯(lián)注入電壓。

2. 就像在射頻放大器中，單根同軸電纜傳輸信號并遠程傳輸功率，使用低通和高通濾波器合并注入的交流信號及其直流成分。

3. 使用真正的電壓加法器。

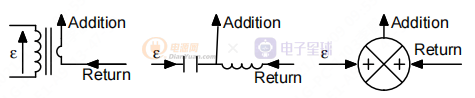圖 8. 注入加法器

對于模擬文件中的第一個解決方案，我們只需在要注入的電線中插入一個純交流電源。 對于實際產(chǎn)品中的測量，最常見的方法是通過變壓器操作浮動正弦波發(fā)生器以提供電流隔離。

對于模擬文件中的第二個解決方案，我們使用非常大的組件值來形成一個非常低的交叉頻率濾波器。 一個 1 kH 電感器將阻止交流內容并對直流內容造成短路。 相反，即使在非常低的頻率下，一個 1 kF 的電容器也會阻止直流成分并短路交流成分。 對于測量，由于注入信號頻率在數(shù)十赫茲到數(shù)百赫茲的范圍內，因此很難獲得足夠大的組件，此選項僅適用于仿真目的。

對于第三種解決方案，加法器模塊通常在模擬器庫中可用。 對于測量，我們可以使用運算放大器和一些電阻來構建具有單位增益的放大器。

三、測量

首先，如果我們要測量系統(tǒng)，我們需要在不影響運行環(huán)境的情況下注入信號。 在我們打破環(huán)路的那一點，我們必須注意阻抗匹配。 這種說法意味著注入加法器的輸入阻抗與斷點處的阻抗匹配，而注入加法器的輸出阻抗與斷點相同 在斷點處。

圖 9. 阻抗匹配原理

為了簡化這些條件，我們可以選擇輸入阻抗無窮大或輸出阻抗為零的斷點。

理論上，理想的運算放大器沒有輸入阻抗（它是開路輸入），也沒有輸出阻抗。

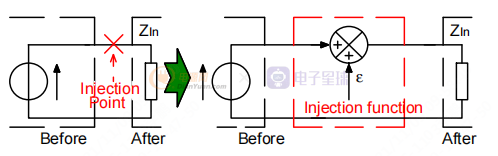圖 10. 運算放大器阻抗匹配

如果環(huán)路中有運算放大器，則滿足此條件。 事實上，運算放大器輸出阻抗幾乎為零（或低于 1Ω）。 一般情況下，運放輸出負載在kΩ范圍內。

圖 11. 斷開運算放大器的環(huán)路

在許多情況下，運算放大器輸出連接在 PWM 設備內部，因此不可能在該點斷開環(huán)路。 一種解決方案包括在輸出處中斷循環(huán)。 通常，輸出阻抗很低，而測量網(wǎng)絡輸入阻抗很高。因此，我們可以使用該點，因為它幾乎就像一個電壓源。 這只會引入與輸出與輸入阻抗之比成正比的小誤差。

圖 12. 在輸出端斷開環(huán)路

在仿真中，我們也必須關心阻抗匹配，但一般情況下，放大器輸出是可用的。其次，為了確保足夠的測量條件，我們必須確保系統(tǒng)保持在線性區(qū)域。如果注入信號是正弦波，則所有其他信號（特別是加法和返回）也應該是正弦波。因此，我們需要為 ε 使用一個較小的值。但是，如果調制幅度太小，則不會無法正確觀察關鍵信號，因為它們會淹沒在環(huán)境中。

在這種情況下，測量是不可能的。因此，調制電平應具有足夠的幅度以保持在本底噪聲之上。為了簡化測量過程，我們可以使用現(xiàn)代示波器提供的一些功能，例如平均、同步檢測或高級觸發(fā)。

在仿真中，隨著程序線性化在運行小信號分析之前的電路中，幅度無關緊要，結果不取決于注入信號幅度。在任何情況下，測量或仿真都不應依賴于環(huán)路中的注入加法器、注入加法器設置和注入信號幅度。如果動態(tài)結果隨著調制幅度的變化而變化太大，則表明系統(tǒng)未在其線性區(qū)域中運行，可能需要調整設置。

四、結果

根據(jù)可用信號，還可以繪制（通過測量或模擬）其他傳遞函數(shù)。 唯一的條件是注入加法器在我們想要繪制的傳遞函數(shù)之外。例如，觀察輸出與驅動的比率將為您提供工廠傳遞函數(shù) H。這很明顯，這里最困難的一點是訪問 驅動信號。如果注入加法器連接到輸出（在這種情況下，返回 = 輸出），如果我們繪制驅動/加法，我們會得到補償器乘以比例因子 (-KC) 的相反結果，因為比較器位于 路徑內。