首先回顧一下傅里葉變換

以方波為例，近似認為任何波形都可由不同頻率、幅值和相位的正弦波組合而成，傅里葉變換就是將任意波形（這里的方波）中的各分量分離出來。如何分離？硬件上可以采用窄帶濾波器，但實際上硬件開銷是難以接受的，通常采用的是數(shù)學方法——歐拉濾波器。

歐拉公式

歐拉公式展示了一根螺旋上升的曲線（如同彈簧），這根神奇的“彈簧”或許更加接近事物的本質，我們通常所能觀察到的或許只是這個三維模型的某個投影。

這里就是借用這個三維歐拉模型來分離頻域中的各個分量實現(xiàn)濾波效果。

設一個頻率為f0=0.3Hz正弦波信號其時域、頻域圖如下：

                                              圖1-1  0.3Hz正弦波時域、頻域圖

如圖把時域信號乘以歐拉公式再積分取模就得到了頻域信號，這一步又稱卷積。這時腦袋里就產生了問號，啥是卷積？為啥歐拉公式能濾波？復數(shù)怎么算？渣一樣的數(shù)學水平是不可能理解這個方程了，那么就換一個角度看看能不能把這個方程的軌跡描繪出來，通過過程說不定就能夠理解這個方程的機理。

一個時域信號乘以歐拉公式后是怎么的軌跡？取歐拉公式中的頻率也為f0=0.3Hz，復平面圖形如下：

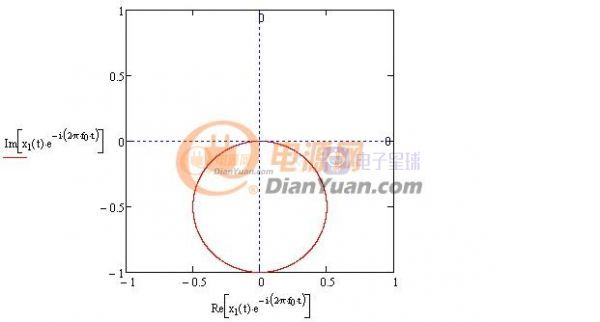
                                         圖1-2  f0=0.3Hz復平面圖

在三維模型中的軌跡如下：

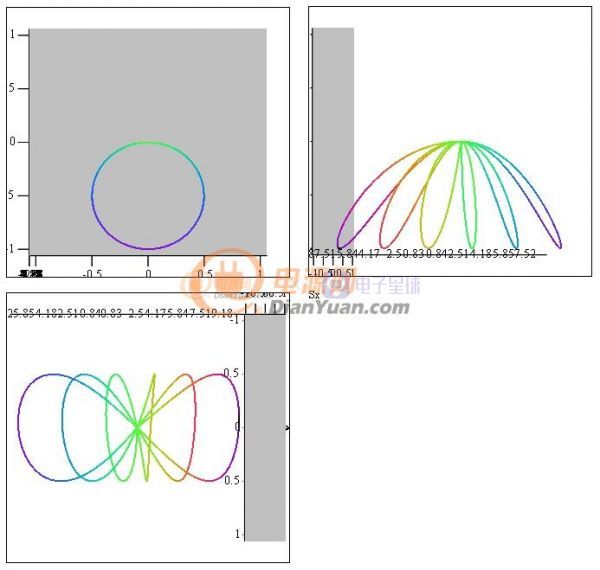
                                               圖1-3 三視圖

三視圖中灰色的是XY平面（復平面），實際發(fā)現(xiàn)Z軸（時間軸）上的數(shù)值對結果沒有影響，只需關心在XY平面的投影即可。從這里看似乎復平面二維圖就足夠了。

  接著用歐拉濾波器進行掃頻觀察復平面、三維圖中軌跡的變化：

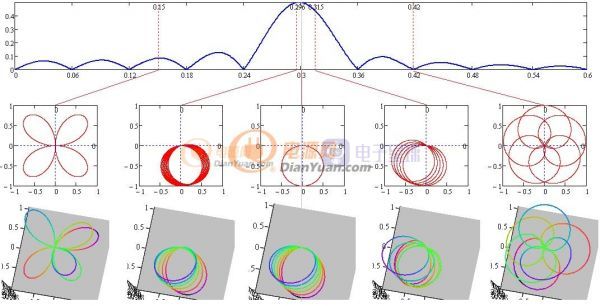
                                      圖1-4 對比頻域中各頻率對應的復平面和三維圖

  通過觀察發(fā)現(xiàn)所有軌跡在復平面的投影重合度越高的對應的頻域值越大，比如歐拉濾波器取f0=3Hz時所有軌跡的投影在一個圓上，而偏離f0=3Hz時投影逐漸散開（如同彎曲的彈簧），在f0=0.42Hz處所有投影成對稱狀（復平面有正有負）得到的頻域值為零。

  再觀察最左邊的f0=0.15Hz處，放大如下：

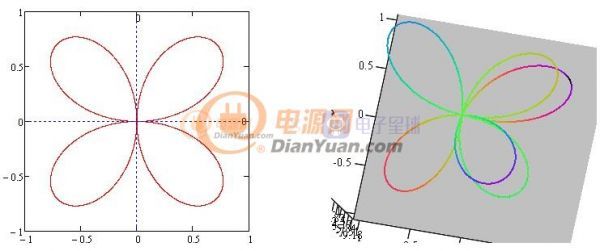
                                                  圖1-4-1 f=0.15Hz放大圖

在復平面中其為對稱圖形得出的頻域值應該為零但實際不為零，通過觀察三維圖右邊的兩個臂為雙重臂所以單純在二維投影中分辨不出來。那么怎樣來求這些投影的重合度？

因為復平面中有正有負當把所有點相加后對稱的部分會抵消掉這樣就能判斷出重合度（或應稱對稱性），再取模就得出了實數(shù)結果。對乘積項進行累加（積分）也就是卷積運算了，卷積運算比較慢有沒有其它更便捷的方法來識別投影的重合度（對稱性）？或者優(yōu)于歐拉濾波器的濾波器？

如果不是單一頻率的波形仍然符合上述規(guī)律只是投影不再是標準的圓形，見下圖：

                                        圖1-5 兩種頻率的合成波頻域及投影

再來分析相位的識別方法，觀察下面不同初始相位時對應的X方向Y方向上投影：

                                               圖1-6-1 0度對應的投影

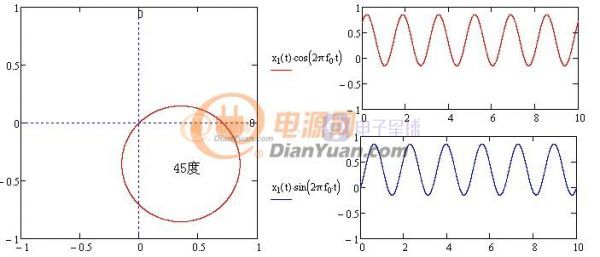
                                                 圖1-6-2 45度對應的投影

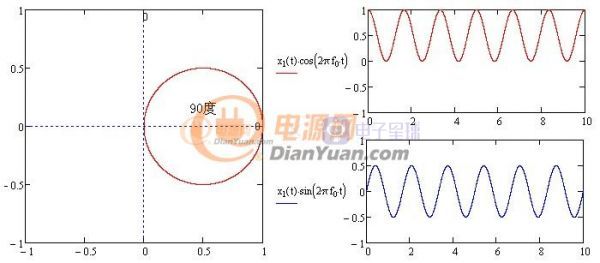
                                                   圖1-6-3 90度對應的投影

通過對比可知初始相位可以用圖中兩條正弦波的均值求反正切獲得，這兩條正弦波為原波形x1(t)分別與歐拉公式的虛部、實部相乘獲得（歐拉三角形式cos(t)-i*sin(t)），平均值可由積分的方法獲得，最終求相位也用到了卷積，表達式及波形如下：

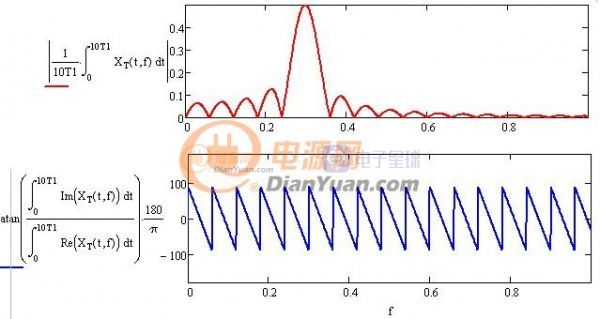
                                                         圖1-7 頻率相位圖

（此處有點小問題，結果相差90度）

傅里葉級數(shù)、傅里葉變換、DFS、DTFT

根據(jù)信號的不同類型，可以把傅立葉變換分為四類：

1) 非周期性連續(xù)信號： 傅立葉變換(Fourier Transform，FT)

2) 周期性連續(xù)信號： 傅立葉級數(shù)(Fourier Series，FS)

3) 非周期性離散信號： 離散時域傅立葉變換(Discrete Time Fourier Transform ,DTFT)

4)周期性離散信號： 離散傅立葉變換(Discrete Fourier Series，DFS)

前面分析的都是周期信號特點時域連續(xù)周期，對應頻域離散非周期屬于傅里葉級數(shù)

                                              圖2-1 傅里葉級數(shù)

對于非周期信號特點時域連續(xù)非周期，對應頻域連續(xù)非周期屬于傅里葉變換

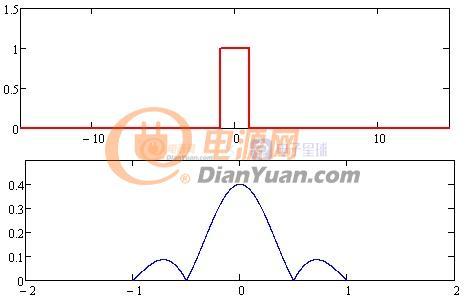
                                                 圖2-2 傅里葉變換

傅里葉變換變換某種程度上可以看做傅里葉級數(shù)在單個峰上的拉伸，雖然y軸值有所不同但頻域反映的是比重似乎影響不大。

前面提到卷積的運算速度比較慢，采用離散化處理后可以減少運算次數(shù)提高運算速度，再者現(xiàn)在的計算機都是數(shù)字計算機對于連續(xù)的模擬數(shù)據(jù)只能抽樣處理。

拉普拉斯變換

在實際波形中會出現(xiàn)不收斂的曲線，這種曲線的軌跡示意如下：

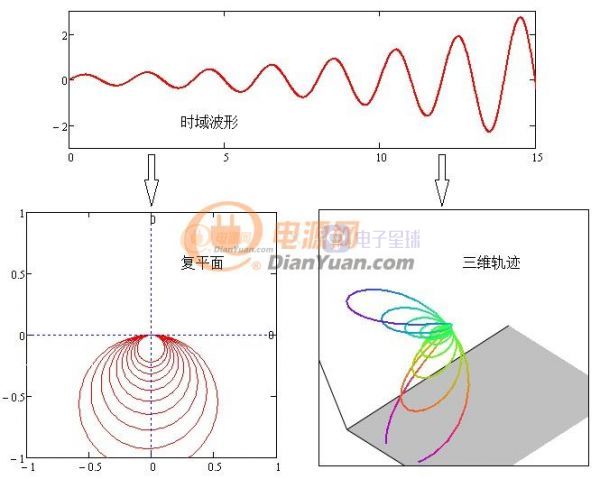
                                                       圖3-1 發(fā)散曲線

從三維圖看沿時間軸方向螺旋半徑越來越大導致積分結果無窮大既不可積，這樣就沒辦法用之前的方法來鑒別頻率了。拉普拉斯先生對此做了改進加入了衰減函數(shù)——e^-σt其中σ為正實數(shù)，為什么用e指數(shù)？有資料說e指數(shù)曲線是自然界衰減最快的曲線。加入這個衰減函數(shù)后的效果如何呢？

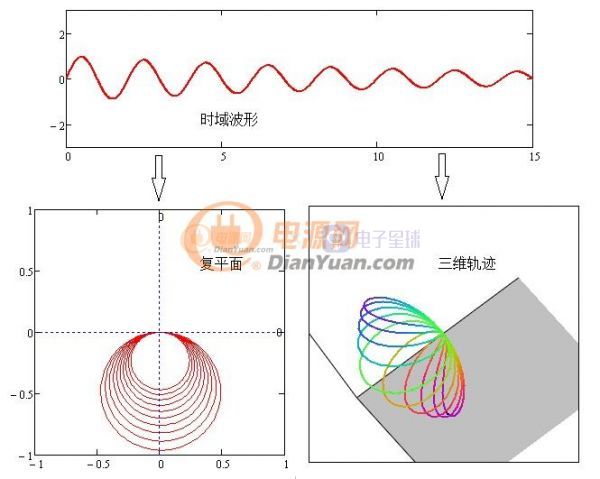
                                                    圖3-2 收斂曲線

這里可以通過調系數(shù)σ來調衰減程度，雖然衰減函數(shù)加在傅里葉公式上，通過公式變換或者實際效果看跟加在時域波形上的效果一樣，換句話說先對時域波形進行收斂處理后再做傅里葉變換等同于拉普拉斯變換。

拉普拉斯變換公式：

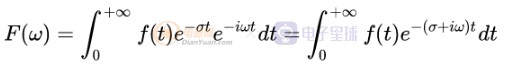
                                                      圖3-3 歐拉濾波器VS拉普拉斯濾波器