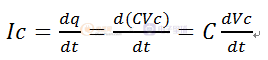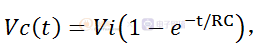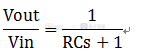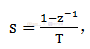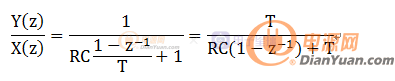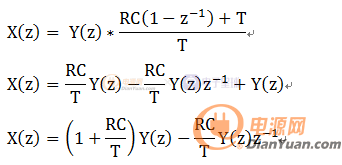第一次發帖,跟在公司寫報告一樣,不知道如何從最簡單的部分展開以及組織語言,大概列個框架,寫寫自己的理解,如果紕漏還請大神們指正~
1、RC低通濾波時域分析
2、RC低通濾波頻域分析
3、軟件上常用濾波算法
4、Z變換(離散化)
沒人看,自己繼續~
1、 RC低通濾波時域分析
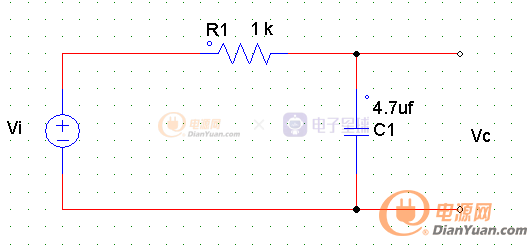
不廢話,先上圖,典型的RC濾波電路如下:
電工們對此電路都極為熟悉吧,不管直流、交流、脈沖信號都可以用它,不管什么產品原理圖上必定都有這個玩意,先從我們最初認識它的時域開始吧,盡管現在已經退化到看見一階微分方程就想死的地步^^。
首先電容電流:
根據基爾霍夫電壓定律寫出如下微分方程:
由于Vi 的單位是V,所以RC的單位則是時間,也就是大家熟知的時間常數t = RC。
OK,至此大家是不是覺得一階系統還是相當簡單吧,那么如何求解這一階微分方式還是交給數字本身吧,結果如下:
假設電容初始電壓為0.
Mathcad 計算如下:
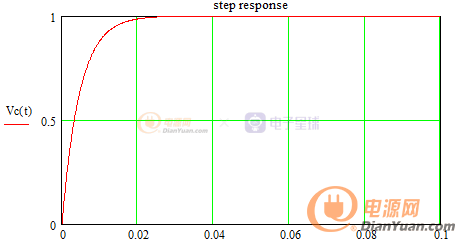
一階RC系統的階躍響應曲線如下:
5.1 這么快就過去了,哎,放假的日子總是這么短暫,憂傷之余還是趕緊來更帖子~
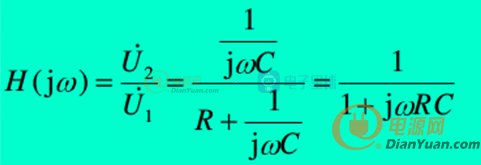
2、 RC低通濾波頻域分析
圖1簡化如下,
以電容電壓為輸出,電路的網絡函數為:
令:則幅值和相角函數如下:
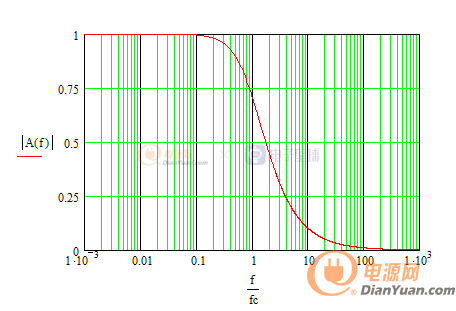
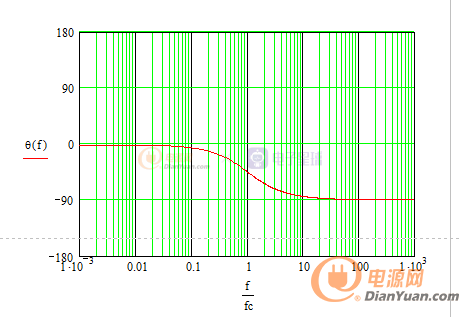
根據上邊公式畫出一階RC低通濾波的幅頻和相頻特性曲線,Mathcad計算如下:
幅頻特性曲線改用對數坐標如下:
如上幅頻和相頻特性曲線,
當w
當w>>Wc時,是斜率與-20dB/十倍頻成比例的一條直線。
當w=Wc時,增益衰減至0.707,即-3dB,相位滯后45°,對于低通濾波器,該頻率通常被稱為截止頻率。
人氣不多,謝謝娜姐給上了首頁,動力十足呀
頻域大家搞電源的接觸比較多,相對熟悉,我就埋個坑先從軟件上常用的濾波算法說起吧。
3、 軟件上常用濾波算法
當年還是菜鳥時,在網上流傳有常用的10種軟件濾波算法(最初源自21ic匠人之手),簡單介紹如下:
1) 限幅濾波法
先根據經驗判斷,確定兩次采樣允許的最大偏差值,設為A。
每次檢測到新采樣值時進行判斷:
(1)如果本次新采樣值與上一次濾波效果之差<=A,則本次采樣值有效,令本次濾波結果=新采樣值;
(2)如果本次采樣值與上次濾波結果之差>A,則本次采樣值無效,放棄本次采樣值,本次濾波結果=上次濾波結果。
2) 中位值濾波法
連續采樣N次值,把采樣值按大小排列,取中間值為本次有效值。
3) 算術平均濾波法
連續取N個值進行算術平均運算。
N較大時,信號平滑度較高,但靈敏度較低;N較小,信號平滑度低,但靈敏度較高。
4) 遞推平均濾波法
把連續N個采集值看成一個隊列,每次采集到的新數據放入隊尾,并扔掉原來隊首的數據。把隊列中的N個數據進行平均計算,即可獲得新的濾波結果。
5) 中位值平均濾波法
中位值平均濾波法又稱脈沖干擾平均濾波法,相當于“中位值濾波法”+“算術平均濾波法”。
連續采集N個數據,去掉一個最大和最小值,然后計算N-2個數的平均值。
6) 遞推中位值平均濾波法
相當于“中位值濾波法”+“遞推平均濾波法”。
這種方法把連續N個值看成一個隊列,每次采集到一個新數據放入隊尾,并扔掉原來隊首的值。
把隊列中的N個數據先去掉一個最大值和最小值,然后計算N-2個數據的平均值。
7) 限幅平均濾波法
相當于“限幅濾波法”+“遞推平均濾波法”。
每次采樣先進行限幅處理,再進行隊列平均濾波處理。
8) 一階滯后濾波法
本次結果濾波結果 = a*本次采樣值 + (1-a)*上次結果。
a代表濾波系數,a = 0~1。
只列出8個吧,有興趣的朋友可以參考附件。仔細看上述8種方法,基本都很好理解。
后邊我會針對 中值平均濾波 和 一階滯后濾波 2種重點分析。
=====================================================
不過分析之前,先提出個問題:在一階滯后濾波算法中,
為什么a的值必須在0~1之間?
在0~1之間,a的值到底該怎么選取,如何跟硬件上的RC參數對應起來呢?
這個問題當年困惑了我好久(別笑話俺額),網上也沒有深入講解,這個就是俺發此帖子的初衷,希望大家多討論哈~
上邊的坑先埋著,先從Z變換說起吧~
4、 Z變換(離散化)
頻率分析中一階RC低通濾波在S域的傳遞函數如下:
這里我們采用一階后向差分法進行z變換。
(注:Z變換方式有很多種,如一階前向差分、一階后向差分、雙線性變換法等,不多說了)
Z變換:
代入S域傳遞函數中:
繼續推導如下:
繼續轉化為差分方程:
至此,通過Z變換我們把S域的傳遞函數轉化為時域的差分方程。
這里通過最簡單的一階系統,給大家展現出從模擬到數字轉化的基本過程,后邊所有的開關電源的環路設計無不是在此基礎上延伸展開。
![]() ~
~![]()
![]()